图

在有向完全图中，每两个不同的顶点之间都有两条方向相反的弧（从顶点u到顶点v和从顶点v到顶点u）。

对于 n 个顶点的有向完全图，弧数的计算公式为：弧数=n×(n−1)

---

---

DFS 遍历顺序取决于邻接点的访问顺序，v0 的邻接点有 3 个，排列组合共 3! = 6 种，但部分排列会生成相同序列

---

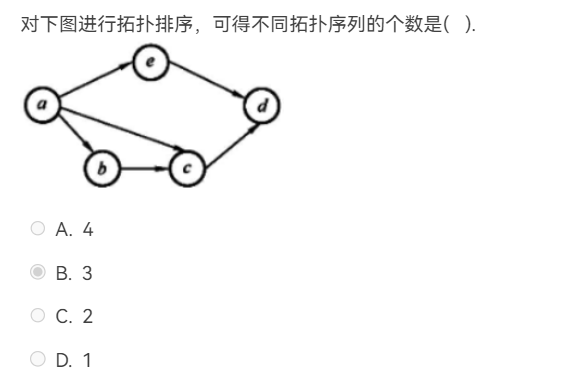
\(a, b, c, e, d\) \(a, e, b, c, d\) \(a, e, c, b, d\) 

---

Prim 算法是从一个顶点开始，不断添加与已选顶点集关联的最小权值边来扩展生成树；Kruskal 算法是从权值最小的边开始，不断添加不构成回路的边来构建生成树。对于一些图，使用这两种算法得到的最小生成树可能是相同的。

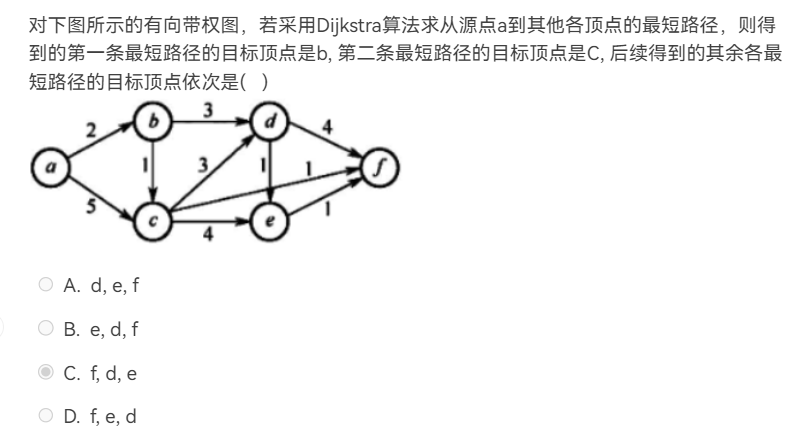
Dijkstra 算法用于求解图中某一特定顶点到其他各顶点的最短路径，采用贪心策略，每次选择距离源点最近且未确定最短路径的顶点。

---

若用邻接矩阵存储有向图，矩阵中主对角线以下的元素均为零，则关于该图拓扑序列的结论是(存在，可能不唯一 )

---

---

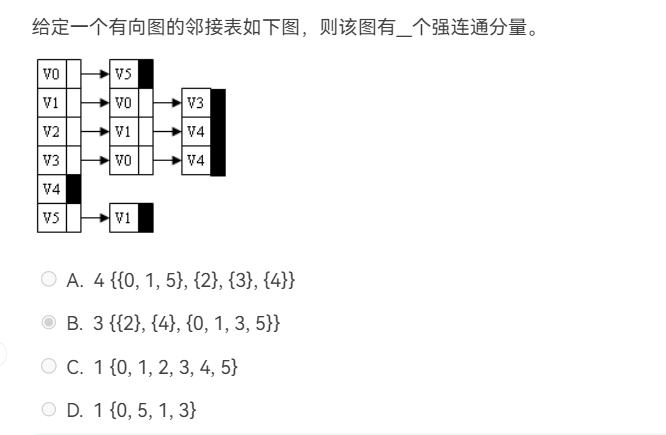
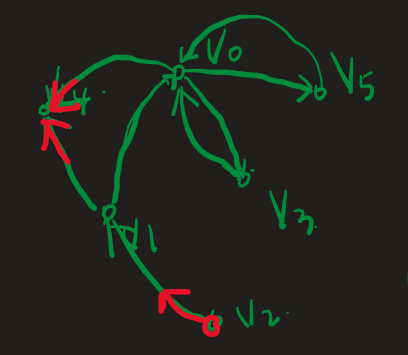
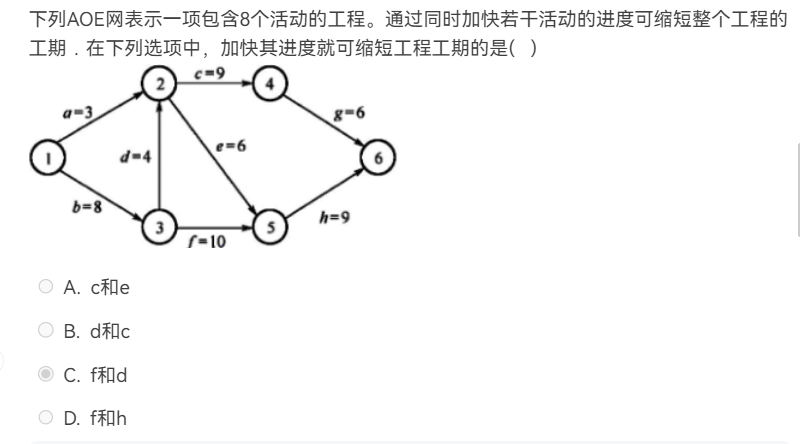
在 AOE 网（边表示活动的网）中，关键路径决定了整个工程的工期，只有加快关键路径上活动的进度，才可能缩短工程工期。
确定关键路径：计算各事件的最早发生时间ve和最迟发生时间vl。事件的最早发生时间ve是从源点到该事件的最长路径长度；事件的最迟发生时间vl是在不影响整个工程工期的前提下，该事件最迟发生的时间。对于活动i，若其开始事件为j，结束事件为k，活动持续时间为wjk，则活动i的最早开始时间e(i)=ve(j)，最迟开始时间l(i)=vl(k)−wjk。当e(i)=l(i)时，该活动是关键活动，由关键活动组成的路径就是关键路径。

---

已知无向连通图G中各边的权值均为1。在下列算法中，一定能够求出图 G中从某顶点到其余各顶点最短路径的是(仅III )。
I. Prim 算法 II. Kruskal 算法 III. 图的广度优先搜索算法

图的创建（邻接矩阵）

本题要求建立一个无向图，采用邻接矩阵做为存储结构。

int locate(MGraph G,char v)//返回顶点v的下标
{
  int i;
  for(i=0;i<G.vexnum;i++)
    if(G.vexs[i]==v)
       return i;
   return -1;
}
void CreatMGraph(MGraph &G)
{
    int i,j,k;
    char v1,v2;
    scanf("%d%d",&G.vexnum,&G.arcnum);
    getchar();
    for(i=0;i<G.vexnum;i++)
         scanf("%c",&G.vexs[i]);
    for(i=0;i<G.vexnum;i++)
         for(j=0;j<G.vexnum;j++)
            G.arcs[i][j]=0;
    for(k=0;k<G.arcnum;k++) {
         getchar();
        scanf("%c%c",&v1,&v2);
        i=locate(G,v1);
        j=locate(G,v2);
        G.arcs[i][j] = 1; 
        G.arcs[j][i] = 1; 
    }
}

---

图的创建-邻接表

本题要求建立一个无向图，采用邻接表做为存储结构。

int locate(ALGraph G,char v);
void CreatMGraph(ALGraph &G) {
    int i, j, k;
    ArcNode *p;
    char v1, v2;
    
    // 输入顶点数和边数
    scanf("%d %d", &G.vexnum, &G.arcnum);
    getchar(); // 消耗掉换行符
    
    // 输入顶点信息，初始化头结点数组
    for (i = 0; i < G.vexnum; i++) {
        scanf("%c", &G.vertices[i].data);
        G.vertices[i].firstarc = NULL;
    }
    getchar(); // 消耗掉换行符
    
    // 输入边的信息，建立邻接表
    for (k = 0; k < G.arcnum; k++) {
        v1 = getchar();
        v2 = getchar();
        getchar(); // 消耗掉换行符
        
        // 查找顶点v1和v2的位置
        int i, j;
        for (i = 0; i < G.vexnum; i++) {
            if (G.vertices[i].data == v1) break;
        }
        for (j = 0; j < G.vexnum; j++) {
            if (G.vertices[j].data == v2) break;
        }
        
        // 生成一个新的表结点
        p = (ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex = j;           // 邻接点序号为j
        
        // 将新结点插入到顶点vi的边表头部
        p->nextarc = G.vertices[i].firstarc;
        G.vertices[i].firstarc = p;
        
        // 若是无向图，还需生成一个对称的边
        p = (ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex = i;           // 邻接点序号为i
        
        // 将新结点插入到顶点vj的边表头部
        p->nextarc = G.vertices[j].firstarc;
        G.vertices[j].firstarc = p;
    }
}

---

孤勇者探险（图的遍历）

一款名为“孤勇者探险”的游戏，游戏中共有若干个小岛，每个岛上均有怪兽，闯关者打倒岛上的怪兽则可获得该岛对应的游戏积分（每个岛的积分根据难度可能不相同），编写程序求出最终闯关成功者（闯过所有小岛）共获得多少积分，并给出对应的闯关行进路线。
思路提示：
游戏地图可抽象为图结构，且一定为连通图。图中顶点的值则为每个小岛对应的积分，‘0’小岛为起点，从0号开始遍历，将各个顶点的值累加则为最终获得得分，同时输出遍历序列，则为对应的闯关行进路线。

void CreateUDG(AMGraph &G)
{
    int i=0;
    int j;
    scanf("%d",&G.vexs[i]);
    G.vexnum=0;
    while(G.vexs[i]!=-1)
    {
        i++;
		scanf("%d",&G.vexs[i]);
        G.vexnum++;
    }
    for(i=0;i<G.vexnum ;i++)
    {
        for(j=0;j<G.vexnum;j++)
        {
            G.arcs[i][j]=0;
        }
    }
    int v1,v2;
    G.arcnum=0;
    scanf("%d %d",&v1,&v2);
    while((v1 != -1) && (v2 != -1))
    {
        G.arcs[v1][v2]=1;
        G.arcs[v2][v1]=G.arcs[v1][v2];
        G.arcnum++;
        scanf("%d %d",&v1,&v2);
    }
}
int DFS(AMGraph G, int v)
{
    int cnt=0;
    printf("%d ",G.vexs[v]);
    cnt+=G.vexs[v];
    visited[v]=1;
    int i;
    int k=0;
    for(i=0;i<G.vexnum;i++)
    {
        if((G.arcs[v][i]!=0) && (!visited[i]))
        {
            k=DFS(G,i);
            cnt+=k;
        }
    }
    return cnt;
}

---

图的广度遍历-邻接表实现

void BFS(ALGraph *G, int v) {
    int queue[MAX_VERTEX_NUM];
    int front = 0, rear = 0;
    
    visited[v] = TRUE;
    queue[rear++] = v;
    
    while (front < rear) {
        int u = queue[front++];
        printf(" %d", u);
        ArcNode *p = G->vertices[u].firstarc;
        while (p != NULL) {
            int w = p->adjvex;
            if (!visited[w]) {
                visited[w] = TRUE;
                queue[rear++] = w;
            }
            p = p->nextarc;
        }
    }
}

---

判断是否唯一拓扑序列（408）

请设计算法：int uniquely(MGraqh G)，判定 G 是否存在唯一的拓扑序列，若是，则返回 1, 否则返回0。

#include <stdlib.h>
int uniquely(MGraph G) {
    int inDegree[MVNum] = {0};
    int queue[MVNum];
    int front = 0, rear = 0;
    int count = 0;
    // 计算每个顶点的入度
    for (int j = 0; j < G.vexnum; j++) {
        for (int i = 0; i < G.vexnum; i++) {
            if (G.arcs[i][j] == 1) {
                inDegree[j]++;
            }
        }
    }
    // 初始化队列，将入度为0的顶点入队
    for (int i = 0; i < G.vexnum; i++) {
        if (inDegree[i] == 0) {
            queue[rear++] = i;
        }
    }
    while (front < rear) {
        // 若队列中元素数量超过1，说明拓扑序列不唯一
        if (rear - front > 1) {
            return 0;
        }
        int u = queue[front++];
        count++;
        // 减少邻接顶点的入度，并将入度变为0的顶点入队
        for (int v = 0; v < G.vexnum; v++) {
            if (G.arcs[u][v] == 1) {
                inDegree[v]--;
                if (inDegree[v] == 0) {
                    queue[rear++] = v;
                }
            }
        }
    }
    // 若拓扑排序无法包含所有顶点，说明图中存在环
    if (count != G.vexnum) {
        return 0;
    }
    return 1;
}

---

最小生成树（普里姆算法）

#include <iostream>
#define MVNum 100
#define MaxInt 32767 
using namespace std;

struct edge{
    char adjvex;
    int lowcost;
}closedge[MVNum];

typedef struct{ 
    char vexs[MVNum];   
    int arcs[MVNum][MVNum]; 
    int vexnum,arcnum;
}AMGraph;

int LocateVex(AMGraph G , char v);//实现细节隐藏
int CreateUDN(AMGraph &G);//实现细节隐藏

int Min(AMGraph G){
    int i;
    int index = -1;
    int min = MaxInt;
    for(i = 0 ; i < G.vexnum ; ++i){
        if(closedge[i].lowcost != 0 && closedge[i].lowcost < min){
            min = closedge[i].lowcost;
            index = i;
        }
    }
    return index;
}

void MiniSpanTree_Prim(AMGraph G, char u){ 
    int k , j , i;
    char u0 , v0;
    k =LocateVex(G, u);
    for(j = 0; j < G.vexnum; ++j){ 
        if(j != k){  
            closedge[j].adjvex =u ;
            closedge[j].lowcost = G.arcs[k][j];
        }
    }
    closedge[k].lowcost = 0;
    for(i = 1; i < G.vexnum; ++i){
        k = Min(G);  
        u0 = closedge[k].adjvex;
        v0 = G.vexs[k]; 
        cout << u0 << "->" << v0 << endl;
        closedge[k].lowcost =0 ; 
        for(j = 0; j < G.vexnum; ++j) 
            if(G.arcs[k][j] < closedge[j].lowcost){
                closedge[j].adjvex = G.vexs[k];
                closedge[j].lowcost = G.arcs[k][j];
            }
    }
}

int main(){
    AMGraph G;
    CreateUDN(G);
    char u;
    cin >> u;
    MiniSpanTree_Prim(G , u);
    return 0;
}

---

最短路径（迪杰斯特拉算法）。

typedef char VerTexType;
typedef int ArcType;

int *D=new int[MVNum];
bool *S=new bool[MVNum];
int *Path=new int[MVNum];

typedef struct{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum,arcnum;
}AMGraph;

int LocateVex(AMGraph G , VerTexType v)//该实现细节隐藏
void CreateUDN(AMGraph &G);//该实现细节隐藏

void ShortestPath_DIJ(AMGraph G, int v0){
int v , i , w , min;
int n = G.vexnum;

for(v = 0; v < n; ++v){
    S[v] = false; 
    D[v] = G.arcs[v0][v];  
    if(D[v] < MaxInt)  Path [v] = v0; 
    else Path [v] = -1;
}

S[v0]=true; 
D[v0]=0; 

for(i = 1;i < n; ++i){ 
    min= MaxInt; 
    for(w = 0; w < n; ++w) 
        if(!S[w] && D[w] < min){
            v = w; 
            min = D[w];
        }          
    S[v]=true; 
    for(w = 0;w < n; ++w)
        if(!S[w] && G.arcs[v][w] != MaxInt &&D[v] + G.arcs[v][w] < D[w]){ 
            D[w] = D[v] + G.arcs[v][w]; 
            Path [w] = v; 
        } 
} 
}

void DisplayPath(AMGraph G , int begin ,int temp ){
if(Path[temp] != -1){
DisplayPath(G , begin ,Path[temp]);
cout << G.vexs[Path[temp]] << "->";
}
}

int main()
{
AMGraph G;
int i , j ,num_start , num_destination;
VerTexType start , destination;
CreateUDN(G);
cin >> start >> destination;
num_start = LocateVex(G , start);
num_destination = LocateVex(G , destination);
ShortestPath_DIJ(G , num_start);
DisplayPath(G , num_start , num_destination);
cout << G.vexs[num_destination]<<endl;
return 0;
}