若栈采用顺序存储方式存储,现两栈共享空间V[1..m],top[i]代表第i个栈( i =1,2)栈顶(该位置不存储对应栈数据),栈1的底在v[1],栈2的底在V[m],则栈满的条件是top[1]-1=top[2]
当两个栈共享一个数组空间时,它们的增长方向是相反的:
栈 1 从数组起始位置(索引 1)开始,向上增长(即栈顶指针top[1]递增)。
栈 2 从数组末尾位置(索引 m)开始,向下增长(即栈顶指针top[2]递减)。
栈满条件推导
栈 1 的有效数据范围:从V[1]到V[top[1]-1]。
例如,当栈 1 为空时,top[1] = 1(无有效数据);当压入一个元素后,top[1] = 2,数据存于V[1]。
栈 2 的有效数据范围:从V[m]到V[top[2]+1]。
例如,当栈 2 为空时,top[2] = m(无有效数据);当压入一个元素后,top[2] = m-1,数据存于V[m]。
栈满的临界条件:
当两个栈的有效数据区域相邻且无间隙时,数组被占满。此时:
栈 1 的最高有效位置为top[1]-1。
栈 2 的最低有效位置为top[2]+1。
若两者相邻,则有:top[1]-1 = top[2]+1 – 1(相邻位置索引差 1),即top[1]-1 = top[2]。
若用大小为6的数组来实现循环队列,且当前front和rear的值分别为0和4。当从队列中删除两个元素,再加入两个元素后,front和rear的值分别为2和0

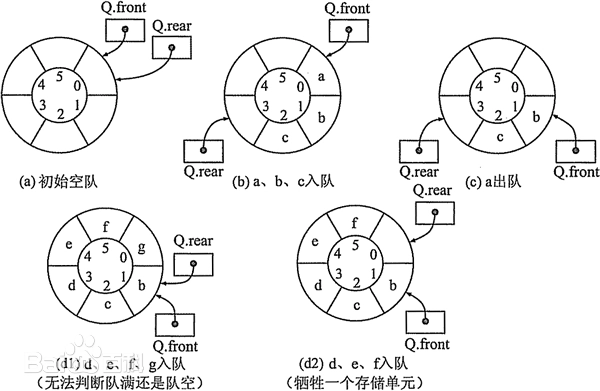

元素个数=(rear−front+队列容量)%队列容量
设C语言数组Data[m+1]作为循环队列SQ的存储空间, front为队头指针,rear为队尾指针,则执行出队操作的语句为front=(front+1)%(m+1)
为解决计算机主机与打印机之间速度不匹配问题,通常设置一个打印数据缓冲区,主机将要输出的数据依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是队列
(SWPU-DS)若串S=“software”,其子串的个数是37。(空串+1)
空串是否计入子串需根据定义判断。若题目未明确包含空串,则总子串数为所有非空长度的子串数之和,即:
总子串数=∑nk=1(n−k+1)=n(n+1)/2;
设栈S和队列Q的初始状态均为空,元素abcdefg依次进入栈S。若每个元素出栈后立即进入队列Q, 且7个元素出队的顺序是bdcfeag, 则栈S的容量至少是3
队列先进先出,栈后进后出

一个栈的入栈序列为1,2, 3,…,n,出栈序列是P1,P2,P3,…,Pn。若P2=3, 则可能取值的个数是n-1
对空栈S进行Push和Pop操作,入栈序列为a,b,c,d,e, 经过Push、Push、Pop、Push、Pop 、Push、Push、Pop操作后得到的出栈序列是b,c,e


已知循环队列存储在一维数组A[0…n-1] 中,且队列非空时front和rear分别指向队首元素和队尾元素。若初始时队列为空,且要求第一个进入队列的元素存储在A[0]处,则初始时 front和 rear 的值分别是0, n-1

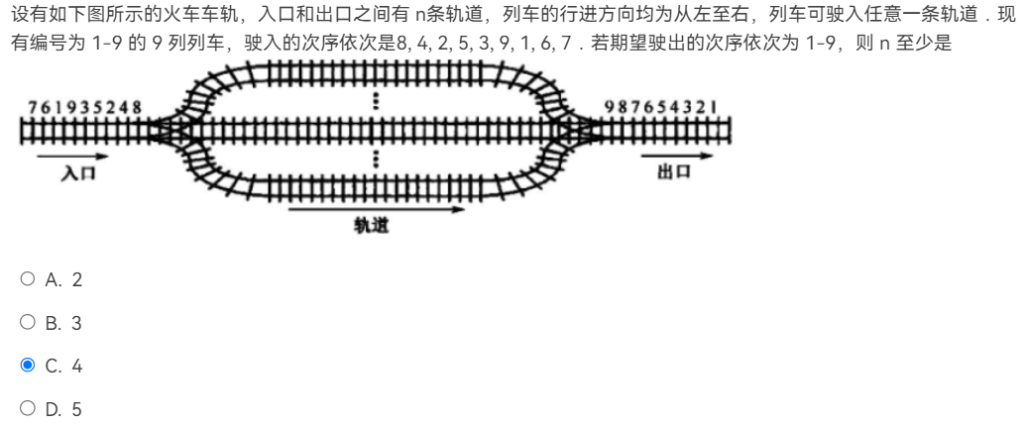
9 8
7 6 5 4
3 2
1
若栈Sl中保存整数,栈S2中保存运算符,函数F( )依次执行下述各步操作:
从Sl 中依次弹出两个操作数a和b.
从S2 中弹出一个运算符op.
执行相应的运算b op a.
将运算结果压入Sl 中.
假定Sl中的操作数依次是5, 8, 3, 2 (2 在栈顶),S2中的运算符依次是*、-、+ (+在栈顶)。调用 3次F( )后,Sl栈顶保存的值是15
与表达式x+y*(z-u)/v等价的后缀表达式是xyzu-*v/+

有一个 12*12 阶对称矩阵M,将其上三角部分的元素mi,j(1<=i<=j<=12)按行优先存入C语言的一维数组N 中,元素m6,6在N 中的下标是50
. 总下标公式(下标从 0 开始)下标=(i−1)×(2n−i)/2+(j−1)
若数组下标从 1 开始,只需在上述公式结果上加 1;

二维数组A按行优先方式存储,每个元素占用1个存储单元。若元素A[0][0] 的存储地址是100, A [3] [3] 的存储地址是220, 则元素A[5] [5] 的存储地址是300
Address(A[i][j])=Base+(i×n+j)×Size
Base=100(A [0][0] 的地址)A [3] [3]=>n=39=>A[5][5]
Size=1(每个元素占 1 个存储单元)
若采用三元组表存储结构存储稀疏矩阵M, 则除三元组表外,下列数据中还需要保存的是仅I、III
I. M的行数 III. M 的列数
–
链队基本操作入队出队
Status InitQueue(LinkQueue &Q) {
Q.front = Q.rear = new QNode;
Q.front->next = NULL;
return OK;
}
Status EnQueue(LinkQueue &Q, QElemType e) {
QueuePtr p;
p = new QNode; // 创建新节点
p->data = e; // 存储数据元素
p->next = NULL;
Q.rear->next=p; // 将新节点链接到队尾
Q.rear=p; // 更新队尾指针指向新节点
return OK;
}
Status DeQueue(LinkQueue &Q, QElemType &e) {
QueuePtr p;
if (Q.front == Q.rear)// 判断队列是否为空
return ERROR; // 队列为空时返回错误
p = Q.front->next; // p指向队头元素(front的下一个节点)
e = p->data; // 获取队头元素的值
Q.front->next=p->next; // 队头指针指向下一个节点
if (Q.rear == p)// 如果删除的是最后一个元素
Q.rear=Q.front; // 重置队尾指针指向头节点
delete p;// 释放被删除节点的内存
return OK;
}
字符串匹配算法
typedef int Status;
#define MAXSTRLEN 255 //用户可在255以内定义最长串长
typedef char SString[MAXSTRLEN+1]; //0号单元存放串的长度
//BF算法
int Index(SString S, SString T, int pos)
{
int i = pos;
int j = 1;
while(i <= S[0] && j <= T[0])
{
if(S[i]==T[j])
{
++i;
++j;
}
else
{
i = i - j + 2;
j = 1;
}
}
if (j > T[0])
return i - T[0];
else
return 0;
return 0;
}编写函数实现顺序栈的初始化、出栈、入栈运算。
Status iniStack(Sqstack &S) //初始化栈
{
S.base=(char*)malloc(stack_INIT_SIZE*sizeof(SElemType));
S.top=S.base;
S.stacksize=stack_INIT_SIZE;
return 1;
}//InitStack
Status push(Sqstack &S,SElemType x)
{
if(S.top-S.base>=S.stacksize) return ERROR;
*S.top++=x;
return OK;
}
Status pop(Sqstack &S,SElemType &e)
{
if(S.top==S.base) return ERROR;
e=*--S.top;
return OK;
}
循环队列出队入队
用一个数组表示循环队列,请编写算法实现循环队列的初始化、入队和出队操作。
输入时:第一行输入队列数据空间容量,第二行依次输入5个待插入元素值,第三行再依次输入5个待插入元素值。
输出时:第一行和最后一行输出循环队列元素值及其下标(元素值(下标)),若中途出现队空或队满,则应给出相应提示。
接口参数: Q是循环队列, N 是队列数组空间容量, x是入队元素, e用于接收出队元素的值
void InitQ(SqQueue &Q,int N){
Q.base = (int *)malloc(N*sizeof(int));
Q.front = Q.rear=0;
}
void AddQ(SqQueue &Q, int x ){
if((Q.rear+1)%N==Q.front){printf("Queue Full\n");
return;
}
Q.base[Q.rear] = x;// 将元素放入队尾位置
Q.rear = (Q.rear+1)%N;// 队尾指针循环后移
}
Status DeleteQ(SqQueue &Q,int &e){
if(Q.front == Q.rear){
printf("Queue Empty\n");
return 0;
}
e=Q.base[Q.front];// 获取队头元素的值
Q.front =(Q.front+1)%N; // 队头指针循环后移
return 1;
}下面程序可实现表达式中括号匹配检查,约定只有‘()’、'[]’、'{}’三种括号。请将以下程序补充完整。
Status push(Sqstack &S,SElemType x) //x入栈S
{
if (S.top - S.base >= S.stacksize) {
S.base = (SElemType *)realloc(S.base, (S.stacksize + stackINCREMENT) * sizeof(SElemType));
if (!S.base) return ERROR;
S.top = S.base + S.stacksize;
S.stacksize += stackINCREMENT;
}
*S.top++ = x;
return OK;
}
Status pop(Sqstack &S,SElemType &e);//从S栈出栈1次元素放入e
Status Compare(char s[]) //s为表达式
{
Sqstack S;
SElemType e;
Status flag = TRUE;
int i = 0;
iniStack(S);
while(s[i] != '#' && flag == TRUE )
{
switch(s[i]){
case '(':
case '[':
case '{':push(S,s[i]);break;
case ')': if(pop(S,e)==ERROR || e != '(')//如果是(
flag = FALSE;break;
case ']': if(pop(S,e)==ERROR || e != '[')//如果是[
flag = FALSE;break;
case '}': if(pop(S,e)==ERROR || e != '{')//如果是{
flag = FALSE;break;
}
i++;
}
if(flag == TRUE && s[i] == '#' && S.top == S.base)
return TRUE;
else
return FALSE;
}许多大学生报名参与大运会志愿者工作。其中运动场引导员需要男女生组队,每组一名男生加一名女生,男生和女生各自排成一队,依次从男队和女队队头各出一人配成小组,若两队初始人数不同,则较长那一队未配对者调到其他志愿者队。现要求写一算法模拟上述配对问题,你需要用队列操作实现上述算法。
Status EnQueue(SqQueue& Q, QElemType e) //入队
{ /* 插入元素e为Q的新的队尾元素 */
if ((Q.rear + 1) % MAX_QSIZE == Q.front) return ERROR;
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAX_QSIZE;
return OK;
}
Status DeQueue(SqQueue& Q, QElemType& e) //出队
{ /* 若队列不空,则删除Q的队头元素,用e返回其值,并返回OK;否则返回ERROR */
if (Q.front == Q.rear) return ERROR;
e = Q.base[Q.front];
Q.front = (Q.front + 1) % MAX_QSIZE;
return OK;
}
void Partner(int num) { //num是志愿者总人数
InitQueue(Mdancers); //男生队列初始化
InitQueue(Fdancers); /女生队列初始化
QElemType p;
for (int i = 0; i < num; i++) //依次将志愿者根据其性别入队
{
cin >> p.name >> p.sex;
if (p.sex == 'F')
EnQueue(Fdancers, p); //插入女队
else
EnQueue(Mdancers, p); //插入男队
}
if (QueueEmpty(Fdancers) || QueueEmpty(Mdancers))
cout << "配对失败!" << endl;
else
{
cout << "配对成功小组:" << endl;
while (!QueueEmpty(Fdancers) &&!QueueEmpty(Mdancers)) { //依次输出男女志愿者的姓名
DeQueue(Fdancers, p); //女生出队
cout << p.name << " "; //输出出队女生姓名
DeQueue(Mdancers, p); //男生出队
cout << p.name << endl; //输出出队男生姓名
}
}
}
编写程序实现银行排队叫号系统,采用链队列作为存储结构。
Status InitLinkQueue(LinkQueue &Q) {
Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode));
if (!Q.front) {
exit(OVERFLOW);
}
Q.front->next = NULL;
return OK;
}
Status EnLinkQueue(LinkQueue &Q, QElemType e) {
QueuePtr p = (QueuePtr)malloc(sizeof(QNode));
if (!p) {
exit(OVERFLOW);
}
p->data = e;
p->next = NULL;
Q.rear->next = p;
Q.rear = p;
return OK;
}
Status DeLinkQueue(LinkQueue &Q, QElemType &e) {
if (Q.front == Q.rear) {
return ERROR;
}
QueuePtr p = Q.front->next;
e = p->data;
Q.front->next = p->next;
if (Q.rear == p) {
Q.rear = Q.front;
}
free(p);
return OK;
}
Status QueueEmpty(LinkQueue Q) {
return Q.front == Q.rear ? TRUE : FALSE;
}
后缀式求值(一位整型操作数版)
我们人类习惯于书写“中缀式”,如 3 + 5 * 2 ,其值为13。 (p.s. 为什么人类习惯中缀式呢?是因为中缀式比后缀式好用么?)
而计算机更加习惯“后缀式”(也叫“逆波兰式”,Reverse Polish Notation)。上述中缀式对应的后缀式是: 3 5 2 * +
现在,请对输入的后缀式进行求值。为了简化输入处理和运算,运算数(操作数)不超过300个且均为1位正整数,运算符(操作符)仅有+ – * /(加减乘除)四种,运算数和运算符之间没有空格间隔,且题目保证运算的中间结果和最终结果都在整型范围内。
但是注意,题目输入的后缀式可能错误,例如:
1234+- 错误,缺少运算符
123+-* 错误,缺少运算数
122-/ 错误,除数为0
题目保证以上三种错误不会同时发生。
#include<bits/stdc++.h>
using namespace std;
stack<int> ans;
int main()
{
int n;
cin >> n;
while(n --) {
string s;
cin >> s;
int num = 0, way = 0;
bool flag = 0;
for(int i = 0; i < s.size(); i ++) {
if(s[i] >= '0' && s[i] <= '9') {
num ++;
}
if(s[i] == '+' || s[i]== '-' ||s[i] == '*' || s[i] == '/') {
way ++;
}
}
if(num - way != 1) {
cout << "Expression Error!" << endl;
continue;
}
for(int i = 0; i < s.size(); i ++) {
if (s[i] >= '0' && s[i] <= '9') {
ans.push(s[i] - '0');
}
if (s[i] == '+') {
int a = ans.top();
ans.pop();
int b = ans.top();
ans.pop();
ans.push(a + b);
}
else if (s[i] == '-') {
int a = ans.top();
ans.pop();
int b = ans.top();
ans.pop();
ans.push(b - a);
}
else if (s[i] == '*') {
int a = ans.top();
ans.pop();
int b = ans.top();
ans.pop();
ans.push(b * a);
}
else if (s[i] == '/') {
int a = ans.top();
ans.pop();
int b = ans.top();
ans.pop();
if (a) {
ans.push(b / a);
}
else{
cout << "Division By Zero!" << endl;
flag = 1;
break;
}
}
}
if (flag) {
continue;
}
cout << ans.top() << endl;
}
return 0;
}