一个二叉树第i层的最大结点数为2^(i-1) i>=1;
深度为k的二叉树有最大结点总数为2^(k-1) k>=1;
对任何非空二叉树,若n0表示叶结点的个数,n2是度为二的非叶结点个数,那么两者满足关系n0=n2+1;
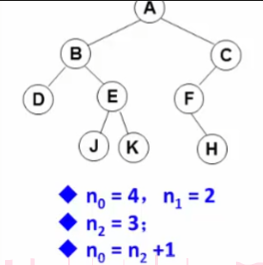


在二叉树结点的先序序列、中序序列和后序序列中,所有叶子结点的先后顺序是 完全相同 的
一棵有n个结点的二叉树,按层次从上到下,同一层从左到右顺序存储在一维数组A[1..n]中,则二叉树中第i个结点(i从1开始用上述方法编号)的右孩子在数组A中的位置( 条件不充分,无法确定 )。


高度为8的完全二叉树至少有( 64 )个叶子结点。
高度为 n的完全二叉树至少有 2n−2个叶子结点(n≥2)。
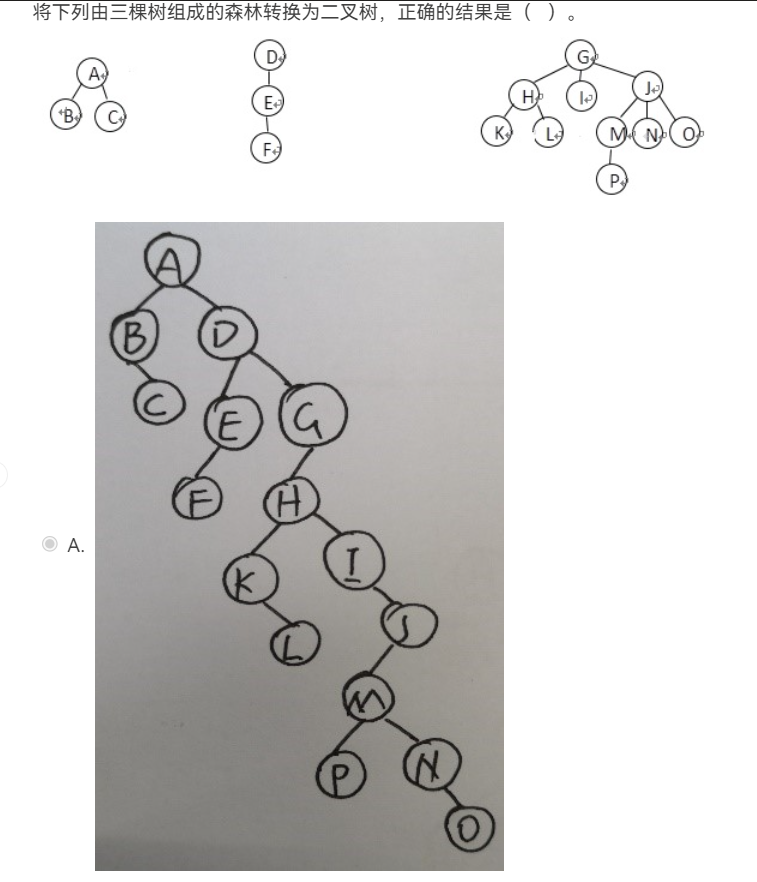
设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。与森林F对应的二叉树根结点的右子树上的结点个数是M2+M3
在二叉树结点的先序序列,中序序列和后序序列中,所有叶子结点的先后顺序完全相同
一个深度为k的,具有最少结点数的完全二叉树按层次,(同层次从左到右)用自然数依此对结点编号,则编号最小的叶子的序号是2 k−2+1
最短。正确的哈夫曼树(要求左孩子权值小于等于右孩子)以及编码是( )。
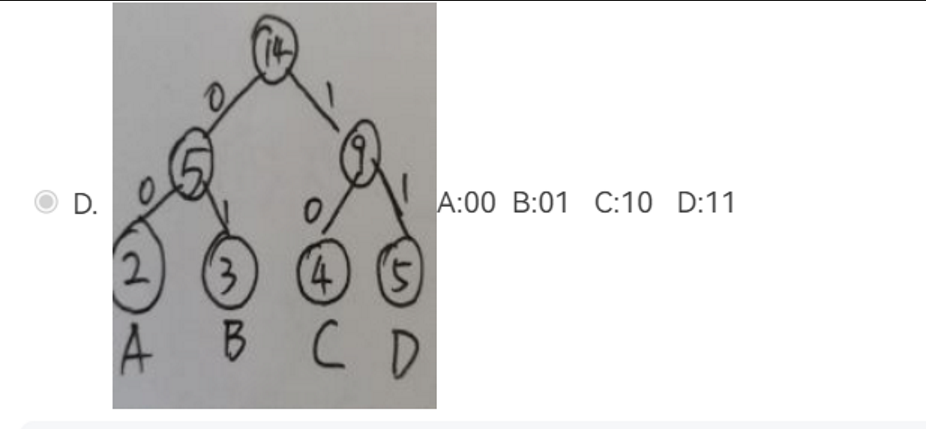
已知一棵完全二叉树的第 6层(设根为第1层)有8个叶结点,则该完全二叉树的结点个数最多是111
叶子节点:也称为终端节点,没有子树的节点或者度为零的节点
第五层及以上是满二叉树 结点数为(2^n)-1
第七层有24*2个结点
最多为前6层结点加未知的数量 2^6-1+48=111


性质1:二叉树的第i层上至多有2^(i-1)(i≥1)个节点
性质2:深度为h的二叉树中至多含有(2^h)-1个节点
性质3:若在任意一棵二叉树中,有n0个叶子节点,有n2个度为2的节点,则必有n0=n2+1
性质4:具有n个节点的满二叉树深为log2(n+1)
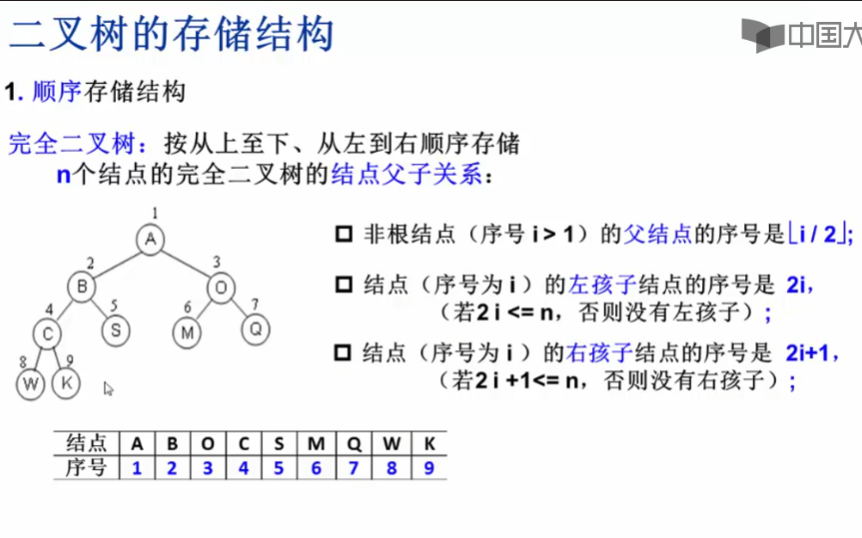
性质5:若对一棵有n个节点的完全二叉树进行顺序编号(1≤i≤n),那么,对于编号为i(i≥1)的节点:
当i=1时,该节点为根,它无双亲节点 。
当i>1时,该节点的双亲节点的编号为i/2 。
若2i≤n,则有编号为2i的左节点,否则没有左节点 。
若2i+1≤n,则有编号为2i+1的右节点,否则没有右节点 。
若一棵完全二叉树有n个结点,则该二叉树中叶结点的个数是
当n为奇数时:
总节点数n为奇数,说明最后一层结点数为奇数,此时n 1=0,代入得:n 0 = (n+1)/2
当n为偶数时:
总节点数n为偶数,最后一层结点数为偶数,此时n 1=1,代入得:n 0 = 2n−1+1= n/2
设一棵非空完全二叉树T的所有叶结点均位于同一层,且每个非叶结点都有2个子结点。若T有
k个叶结点,则T的结点总数是2k-1

对于任意一棵高度为且有10个结点的二叉树,若采用顺序存储结构保存,每个结点占1个存储单元(仅存放结点的数据信息),则存放该二叉树需要的存储单元数量至少是(2^h)-1

要使一棵非空二叉树的先序序列与中序序列相同,其所有非叶结点须满足的条件是( )
只有右子树


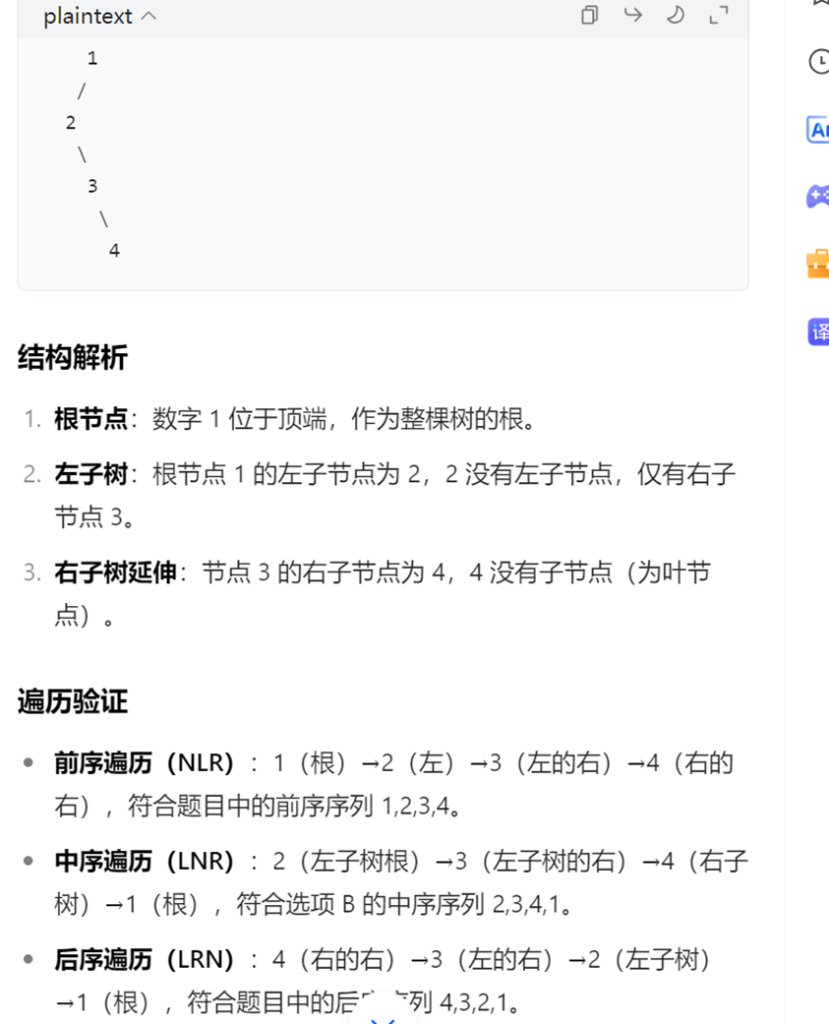



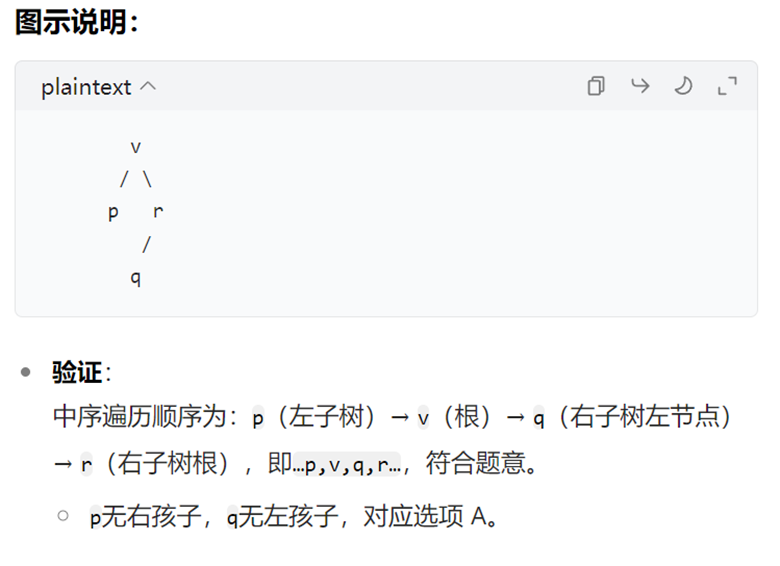


先序序列为 a, b, c, d的不同二叉树的个数是14

卡特兰数应用:对于 n 个节点的二叉树,其形态数满足卡特兰数。当已知先序遍历序列(或后序遍历序列 )时,不同二叉树的个数都可以用卡特兰数计算。因为先序遍历确定了
根节点(第一个元素 ),后续节点在左右子树的分配组合情况符合卡特兰数的规律。
在一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个
度为1的结点,则树T的叶结点个数是82
在无向图中,所有结点的度之和 = 2 × 边数 e
在有根树中,所有结点的出度之和 = 边数 (e)。
设树T的节点总数为N,由上述树的性质可知,边数e=结点数N−1
根据度之和的计算方法,可得度之和为122,节点数为123,
又节点总数N等于度为4、度为3、度为2、度为1和度为0(叶结点)的节点数之和
20+10+1+10+x=123,

已知一棵有2011个结点的树,其叶结点个数为116, 该树对应的二叉树中无右孩子的结点个数是1896
结论:
一棵分支结点(非终端结点)个数为n(总结点数-叶结点数) 的树,该树对应的二叉树中无右孩子的结点(或右指针域为空的结点)个数为 n + 1。【森林对应二叉树时也适用,上述过程推导主要涉及对应后的二叉树】
其他推导中所得的结论:
原始树(或森林)的叶结点个数 = 转换的二叉树中左指针域为空的个数
非空指针域个数 = 总结点个数 – 1
空指针域个数 = 总结点个数 + 1
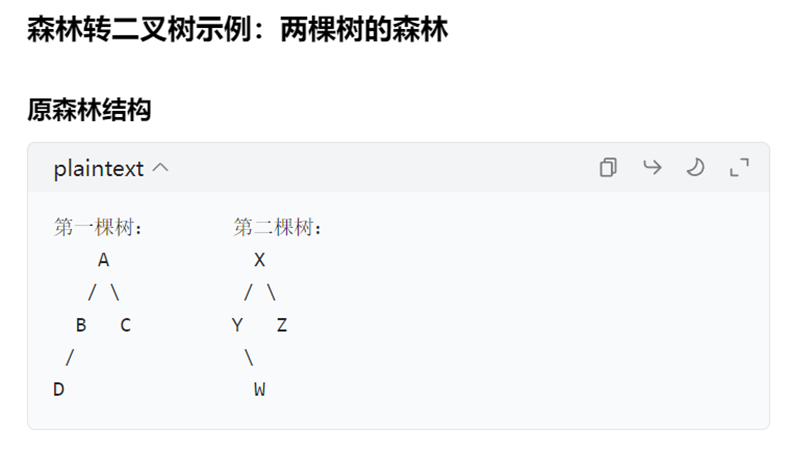
题目:将森林F转换为对应的二叉树T,F中叶结点的个数等于__。【2014年全国试题】
A.T中叶结点的个数
B.T中度为1的结点个数
C.T中左孩子指针为空的结点个数
D.T中右孩子指针为空的结点个数
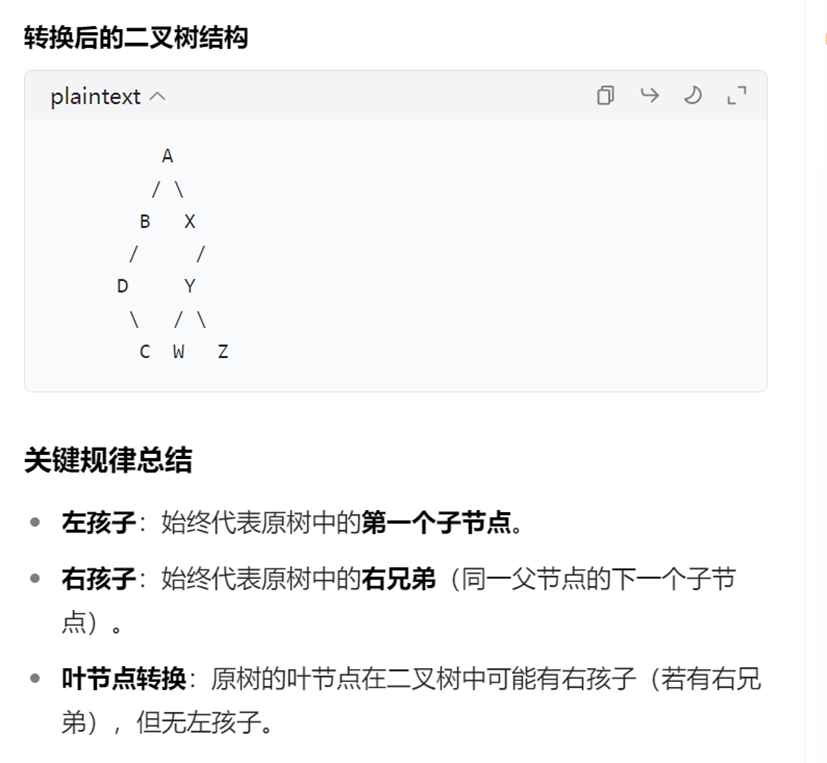
左孩子 – 右兄弟” 规则:树中一个节点的第一个孩子在二叉树中成为其左孩子,这个节点的
右兄弟在二叉树中成为其右孩子
A
/ | \
B C D
/ \ \
E F G
树的说明:根节点为 A,有 3 个子节点 B、C、D;B 有 2 个子节点 E、F;D 有 1 个子节点
G。
A
/
B
/ \
E C
\ \
F D
/
G

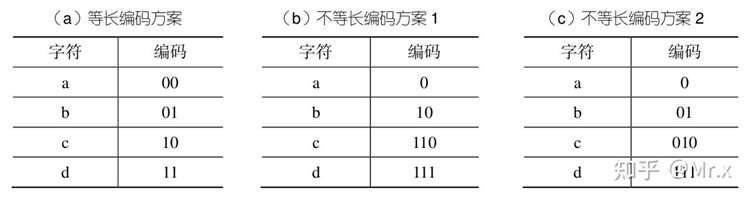
前缀编码的定义
前缀编码要求在一组编码中,任何一个字符的编码都不是其他字符编码的前缀。
左孩子依旧作为左孩子
左孩子的最近的右兄弟作为该左孩子的右儿子
以此类推
对n个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有115个结点,则n的值是58
已知哈夫曼树共有115个结点,即N=115,由N=2n 0 −1可得n 0 = 116/2=58 ,因为n就是叶节点数n 0(n个互不相同的符号对应哈夫曼树的n个叶节点 ),所以n=58。
哈夫曼树的节点数N必为奇数,不可能为偶数。
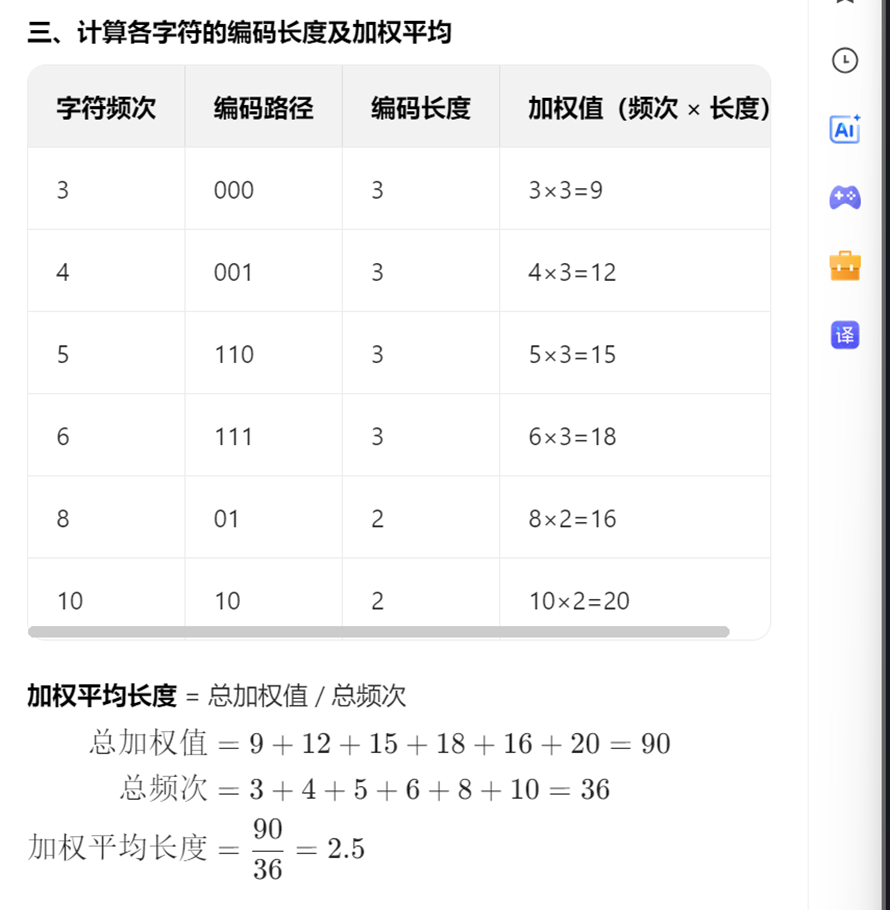
若某二叉树有5个叶结点,其权值分别为10, 12, 16, 21, 30, 则其最小的带权路径长度 (WPL)
是( )



C,n个结点的连通无向图最少需要n−1条边 。可以把无向图想象成树的结构(树是一种特殊的连通无向图),树中节点数为n时,边数恰好是n−1,此时图中每两个顶点之间恰好有一个路径,刚好连通且没有多余的边。当边数小于n−1时,图一定是非连通的 。
统计二叉树度为1的结点个数。
#include<iostream>
using namespace std;
typedef struct BiNode{
char data;
struct BiNode *lchild,*rchild;
}BiTNode,*BiTree;
void CreateBiTree(BiTree &T){
char ch;
cin >> ch;
if(ch=='#') T=NULL;
else{
T=new BiTNode;
T->data=ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
int NodeCount ( BiTree T)
{
if(T==NULL) return 0;
if(T->lchild==NULL&&T->rchild!=NULL)
return 1;
if(T->lchild!=NULL&&T->rchild==NULL)
return 1;
return NodeCount(T->lchild)+NodeCount(T->rchild);
}
int main(){
BiTree T;
CreateBiTree(T);
printf("%d", NodeCount(T));
return 0;
}
计算二叉树深度。
int Depth(BiTree T)
{
int m, n;
if (T == NULL)
return 0;
else
{
m = Depth(T->lchild);
n = Depth(T->rchild);
if (m > n)
return (m + 1);
else
return (n + 1);
}
}
创建哈夫曼树。
#include<cstring>
#include<iostream>
using namespace std;
typedef struct
{
int weight;
int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode;
void Select(HuffmanTree HT,int len,int &s1,int &s2)
{
int i,min1=32767,min2=32767;
for(i=1;i<=len;i++)
{
if(HT[i].weight<min1&&HT[i].parent==0)
{
s2=s1;
min2=min1;
min1=HT[i].weight;
s1=i;
}
else if(HT[i].weight<min2&&HT[i].parent==0)
{ min2=HT[i].weight;
s2=i;
}
}
}
void CreatHuffmanTree(HuffmanTree &HT,int n)
{
int m,s1,s2,i;
if(n<=1) return;
m=2*n-1;
HT=new HTNode[m+1];
for(i=1;i<=m;++i)
{ HT[i].parent=0; HT[i].lchild=0; HT[i].rchild=0; }
for(i=1;i<=n;++i)
cin >> HT[i].weight;
for(i=n+1;i<=m;++i)
{
Select(HT,i-1,s1,s2);;
HT[s1].parent=i;
HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
}
void print(HuffmanTree HT,int n)
{
for(int i=1;i<=2*n-1;i++)
cout << HT[i].weight << " " << HT[i].parent << " " << HT[i].lchild << " " << HT[i].rchild << endl;
}
int main()
{
HuffmanTree HT;
int n;
cin >> n;
CreatHuffmanTree(HT,n);
print(HT,n);
return 0;
}
哈夫曼编码
编写函数实现哈夫曼编码。输入结点个数(保证个数>1)及各结点的权值,为各结点进行编码。
void CreateHuffman_tree(HuffmanTree &HT,int n)
{
if(n<=1)
{
return ;
}
int m=2*n-1;
HT=new HTNode[m+1];
for(int i=0;i<=m;i++)
{
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&HT[i].weight);
}
for(int i=n+1;i<=m;i++){
int s1,s2;
Select(HT,i-1,s1,s2);
HT[s1].parent=i;
HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
}
void Huffman_code(HuffmanTree HT,HuffmanCode &HC,int n)
{
HC=new char*[n+1];
char *s=new char[n];
s[n-1]='\0';
for(int i=1;i<=n;i++)
{
int c,f,start=n-1;
c=i;
f=HT[i].parent;
while(f)
{
--start;
if(HT[f].lchild==c) s[start]='0';
else s[start]='1';
c=f;
f=HT[f].parent;
}
HC[i]=new char[n-start];
strcpy(HC[i],&s[start]);
}
delete s;
}
二叉树的遍历
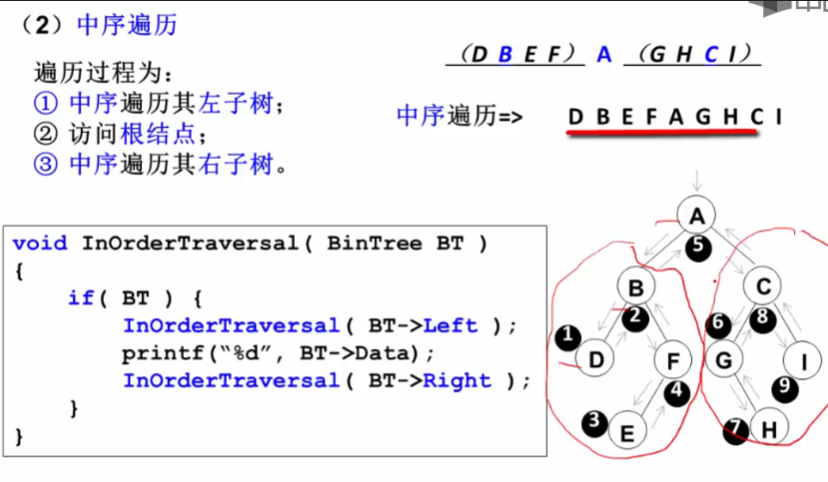
输入二叉树的先序遍历序列,以#代表空树,输出该二叉树的中序遍历序列。例如,有如下二叉树,其先序序列为:ABC##DE#G##F###,输出其中序序列:CBEGDFA
void InOrder(BiTree Tree)
{
if (Tree != NULL)
{
InOrder(Tree->lchild); // 先遍历左子树
printf("%c", Tree->data); // 访问根节点并输出数据
InOrder(Tree->rchild); // 再遍历右子树
}
}
BiTNode* newNode(char data) {
BiTNode* node = (BiTNode*)malloc(len);
node->data = data;
node->lchild = node->rchild = NULL;
return node;
}
void creat(BiTree &Tree)
{
char ch;
scanf("%c",&ch);
if(ch=='#')
{
Tree=NULL;
}
else{
Tree=(BiTNode*)malloc(len);
Tree->data=ch;
creat(Tree->lchild);
creat(Tree->rchild);
}
}
求二叉树的WPL(408)
二叉树的带权路径长度 (WPL) 是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树T, 采用二叉链表存储,结点结构为

其中叶结点的weight域保存该结点的非负权值。设root为指向T的根结点的指针,请设计求T的WPL的算法.
int WPL(BiTree root)
{
if (root == NULL)
{
return 0;
}
BiTree queue[len];
int front = 0, rear = 0;
int wpl = 0;
int depth = 0;
queue[rear++] = root;
while (front != rear)
{
int count = rear - front;
for (int i = 0; i < count; i++)
{
BiTree curr = queue[front++];
if (curr->lchild == NULL && curr->rchild == NULL)
{
wpl += curr->weight * depth;
}
if (curr->lchild != NULL)
{
queue[rear] = curr->lchild;
rear++;
}
if (curr->rchild != NULL)
{
queue[rear] = curr->rchild;
rear++;
}
}
depth++;
}
return wpl;
}
后缀式
本题要求实现一个函数,输出二叉树表示的表达式的后缀式。输入一个表达式的前缀形式(该表达式二叉树的扩展的先序序列),构造该二叉树,并输出其后序序列即为该表达式的后缀形式。
void creat(BiTree &Tree){
char c;
scanf("%c",&c);
if(c=='#'){
Tree=NULL;
}else{
Tree=(BiTree)malloc(len);
Tree->data=c;
creat(Tree->lchild);
creat(Tree->rchild);
}
}
void PostOrder(BiTree Tree){
if(Tree==NULL){
return;
}
PostOrder(Tree->lchild);
PostOrder(Tree->rchild);
printf("%c",Tree->data);
}表达式树转中缀表达式(408)
请设计一个算法,将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。例如,当下列两棵表达式树作为算法的输入时:
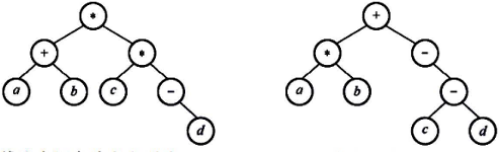
输出的等价中缀表达式分别为 (a+b)* (c* (-d) )和 (a*b) + (- (c-d) )。
二叉树结点定义如下:
typedef struct node{
char data ;
struct node *left, *right;
}BTree;
void Btree(BiTree root, int deep)
{
if (root == NULL)
return ;
else if (root->lchild == NULL && root->rchild == NULL) //叶节点
printf("%c", root->data); //输出操作数
else
{
if (deep > 1)
printf("(");
Btree(root->lchild, deep + 1);
printf("%c", root->data); //输出操作符
Btree(root->rchild, deep + 1);
if (deep > 1)
printf(")");
}
}
void BtreeToE(BiTree root)
{
Btree(root, 1);
}