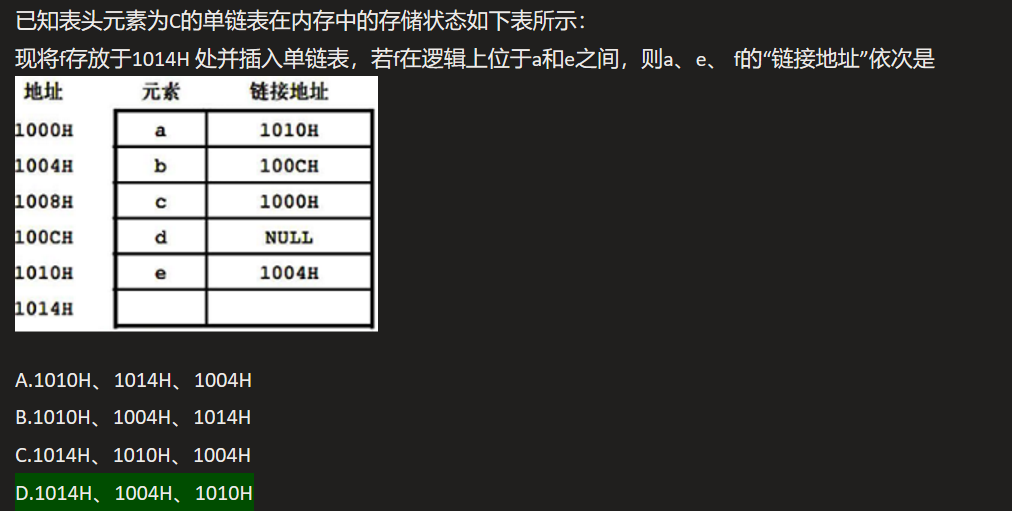
⭕顺序存储表示中数据元素之间的逻辑关系是由( 存储位置)表示的。
⭕在单链表指针为p的结点之后插入指针为s的结点,正确的操作是:
s->next=p->next;p->next=s⭕对于一个头指针为head的带头结点的单链表,判定该表为空表的条件是
head→next==NULL头结点的指针域为空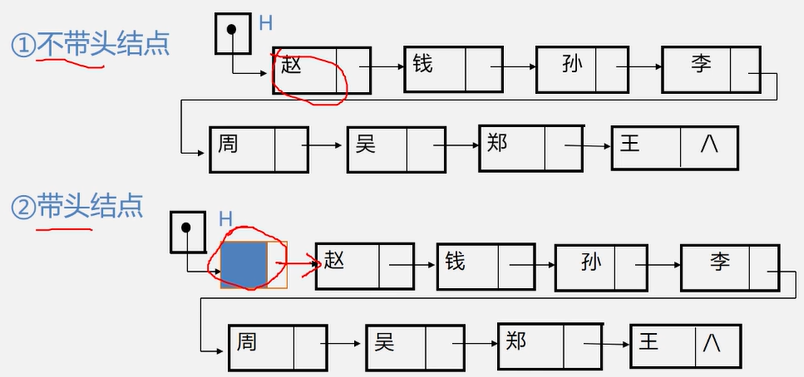
头结点的作用是使所有链表(包括空表)的头指针非空,并使对单链表的插入、删除操作不需要区分是否为空表或是否在第一个位置进行,从而与其他位置的插入、删除操作一致。
⭕将两个结点数都为N且都从小到大有序的单向链表合并成一个从小到大有序的单向链表,那么可能的最少比较次数是:N
⭕在数据结构中,与所使用的计算机无关的是数据的( 逻辑 )结构。
⭕链式存储的存储结构所占存储空间( 分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针 )
⭕线性表L=(a1, a2 ,……,an )用一维数组表示,假定删除线性表中任一元素的概率相同(都为1/n),则删除一个元素平均需要移动元素的个数是((n-1)/2)。
⭕已知头指针h指向一个带头结点的非空循环单链表,结点结构为,其中next是指向直接后继结点的指针,p是尾指针,q是临时指针。现要删除该链表的第一个元素,正确的语句序列是
q=h->next; h->next=q->next; if(p==q) p=h; free(q);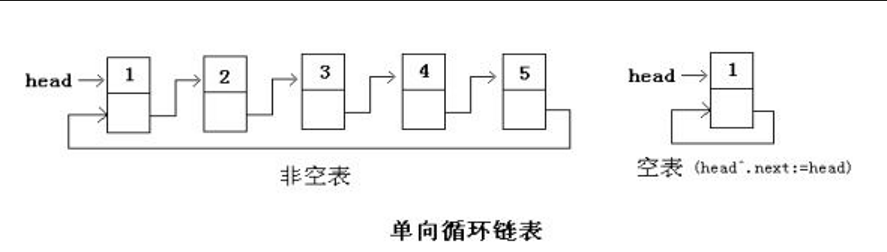
已知一个带有表头结点的循环双链表L, 结点结构为,其中prev和next分别是指向其直接前驱和直接后继结点的指针。现要删除指针p所 指的结点,正确的语句序列是
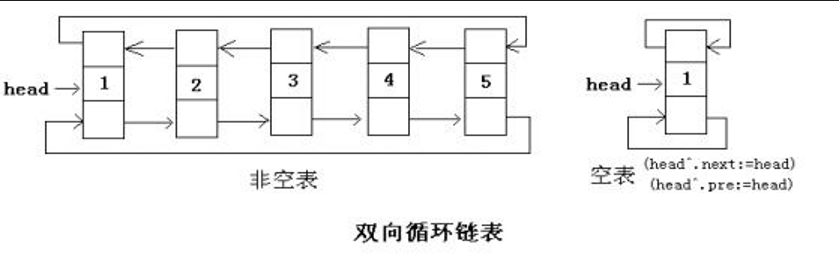
p->next->prev=p->prev; p->prev->next=p->next; free(p);
⭕现有非空双链表 L, 其结点结构为,prev是指向直接前驱结点的指针,next是指向直接后继结点的指针。若要在L中指针p所指向的结点(非尾结点)之后插入指针s指向的新结点,则在执行语句序列 “s->next=p->next; p->next=s;” 后,下列语句序列中还需要执行的是
p->next->prev=s->prev; s->next->prev=p;
已知带头结点的非空单链表L 的头指针为 h, 结点结构为,其中next是指向直接后继结点的指针.现有指针p和q, 若p指向L中非首且非尾的任意一个结点,则执行语句序列“q=p->next; p->next=q->next; q->next= h->next; h->next=q;” 的结果是
将q所指结点移动到L的头结点之后
⭕设一个链表最常用的操作是在末尾插入结点和删除尾结点,则选用( 带头结点的双循环链表 )最节省时间。
⭕若某线性表中最常用的操作是取第i个元素和找第i个元素的前趋元素,则采用( 顺序表 )存储方式最节省时间。
⭕在下列对顺序存储的有序表(长度为 n) 实现给定操作的算法中,平均时间复杂度为O(1)的是
A.查找包含指定值元素的算法
B.插入包含指定值元素的算法
C.删除第i(1≤i≤n)个元素的算法
D.获取第i(1≤i≤n)个元素的算法
以下说法错误的是 ( )。
A.对于线性表来说,定位运算LocateElem在顺序表和单链表上的时间复杂度均为O(n)
C.在链表上实现读表元运算的平均时间复杂度为O(1)
链表中元素不连续存储,读取第 i 个元素时必须从头节点开始遍历,直到找到第 i 个节点,平均时间复杂度为 O (n)。
顺序表的查找操作按元素值查找平均时间复杂度为 O (n)按下标查找时间复杂度为 O (1);插入和删除操作平均时间复杂度为 O (n);获取操作时间复杂度为 O (1)。
链表的插入 / 删除操作在已知相邻节点时效率极高O (1),但查找和随机访问需遍历链表,时间复杂度为 O(n),这是由链表的非连续存储特性决定的。
设 n是描述问题规模的非负整数,下列程序段的时间复杂度是( O(n) )。
x=0;
while (n>=(x+1)*(x+1))
x=x+1;
下列程序段的时间复杂度是( O(n) )。
int sum=0;
for(int i=1;i<n;i*=2)
for(int j=0;j<i;j++)
sum++;
下列程序段的时间复杂度是(O(nlog3n) )。
count=0;
for(k=1;k<=n;k*=3}
for (j=l;j <=n;j++)
count++;
编写函数实现顺序表的初始化和顺序查找。
Status InitList_Sq(SqList &L)
{
L.elem=(ElemType*)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(!L.elem) return OVERFLOW;
L.length=0;
return OK;
}
int Locate(SqList L,ElemType key){
for(int i=0;i<L.length;i++){
if(key==L.elem[i]){
return i;
}
}
return -1;
}本题要求实现一个函数,在顺序表的第i个位置插入一个新的数据元素e,插入成功后顺序表的长度加1,函数返回值为1;插入失败函数返回值为0;
int ListInsert(SqList &L,int i,ElemType e){
if(i<1||i>L.length+1){
return 0;
}
if(L.length>=MAXSIZE){
return 0;
}
for(int j=L.length;j>=i;j--){
L.elem[j]=L.elem[j-1];
}
L.elem[i-1]=e;
L.length++;
return 1;
}本题要求实现一个函数,要求将顺序表的第i个元素删掉,成功删除返回1,否则返回0
int ListDelete(SqList &L,int i){
if(i<1||(i>L.length)) return 0;
for(int j=i;j<=L.length;j++){
L.elem[j-1]=L.elem[j];
}
--L.length;
return 1;
}编写3个函数,分别实现单链表(带头结点)的查询、插入、删除。
int Get_LinkList(LinkList H, ElemType key){
LinkList p;
int i=1;
p=H->next;
while(p!=NULL&&(p->data!=key)){
p=p->next;
i++;
}
if(p==NULL)return 0;
return i;
}//H为单链表的头指针,key为待查找的值;
Status ListInsert(LinkList &H,int i,ElemType e){
LinkList p;
p=H;
if(i<1||i>30)return 0;
for(int j=1;j<i;j++){
if(p==NULL)return 0;
p=p->next;
}
if(p!=NULL){
LinkList addNode=(LinkList)malloc(sizeof(LNode));
addNode->data=e;
addNode->next=NULL;
if(p->next!=NULL){
addNode->next=p->next;
}
p->next=addNode;
return 1;
}
return 0;
}//H为单链表的头指针,i为插入位置,e为新插入的值;
Status ListDelete(LinkList &H,int i){
if(i<1||i>30)return 0;
LinkList p,q;
p=H;
for(int j=1;j<i;j++){
if(p->next==NULL)return 0;
p=p->next;
}
if(p->next==NULL)return 0;
q=p->next;
if(q->next!=NULL){
p->next=q->next;
}
else{
p->next=NULL;
}
free(q);
return 1;
}//H为单链表的头指针,i为删除位置找出数组中未出现的最小正整数(408)
给定一个含n(n≥1)个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如,数组{-5,3,2, 3}中未出现的最小正整数是1;数组{1,2,3}中未出现的最小正整数是4。
int findMissMin(int a[],int n){
int assist[n+1];
memset(assist,0,sizeof(assist));//初始化assist数组(全部元素置为0)
int i;//下标
for(i = 0; i<n ; i++){//遍历数组a,找出小于n+1的整数存入辅助数组
if(a[i]>0&&a[i]<n+1){
assist[a[i]] = 1;//标记值为a[i]的正整数存在
}
}
for(i = 1;i<n+1;i++){//遍历辅助数组,正整数取整为1到n,所以下标遍历是从1到n
if(assist[i] == 0){
break;//说明值为i的正整数未出现过
}
}
return i;
}
顺序表循环左移(408)
设将n (n > 1) 个整数存放到一维数组R 中。设计一个在时间和空间两方面都尽可能高效的算法.将R中保存的序列循环左移p(0<p<n) 个位置,即将R中的数据由(X0,X1,…Xn−2,Xn−1)变换为(Xp,Xp+1,…Xn−1,X0,X1,…Xp−1,)。
void Reverse(int R[], int start, int end) {
while (start < end) {
int temp = R[start];
R[start] = R[end];
R[end] = temp;
start++;
end--;
}
}
Status Converse(int R[], int n, int p) {
if (p <= 0 || p >= n) {
return ERROR;
}
Reverse(R, 0, p - 1);
Reverse(R, p, n - 1);
Reverse(R, 0, n - 1);
return OK;
}
求链表倒数第k个结点(408)
已知一个带有表头结点的单链表,结点结构定义为:
typedef struct LNode
{
ElemType data; //结点数据
struct LNode *next; //结点链接指针
} LNode, *LinkList;在不改变链表的前提下,请设计一个尽可能高效的算法,查找链表中倒数第k个位置上的结点(k为正整数)。若查找成功,算法输出该结点的 data 域的值,并返回1;否则,只返回0.
int Search_k(LinkList list, int k) {
LinkList slow = list->next;
LinkList fast = list->next;
int i;
for (i = 0; i < k; i++) {
if (fast == NULL) {
return 0;
}
fast = fast->next;
}
while (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
if (slow != NULL) {
printf("%d\n", slow->data);
return 1;
}
return 0;
}
链表重排(408)
设线性表L= (a1,a2,a3,…an-2,an-1,an) 采用带头结点的单链表保存,链表中的结点定义如下:
typedef struct node {
int data;
struct node*next;
}NODE;
请设计一个空间复杂度为O(1)且时间上尽可能高效的算法,重新排列L中的各结点,得到线性表L’= (a1,an,a2,an-1,a3,an-2…)。
void change_list(NODE *h) {
if (h->next == NULL || h->next->next == NULL) {
return; // 链表为空或只有一个节点,无需处理
}
// 使用快慢指针找到链表的中间节点
NODE *slow = h->next;
NODE *fast = h->next;
while (fast->next != NULL && fast->next->next != NULL) {
slow = slow->next;
fast = fast->next->next;
}
// 反转后半部分链表
NODE *prev = NULL;
NODE *curr = slow->next;
slow->next = NULL; // 断开前后两部分
while (curr != NULL) {
NODE *next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
// 合并两个链表
NODE *first = h->next;
NODE *second = prev;
while (second != NULL) {
NODE *first_next = first->next;
NODE *second_next = second->next;
first->next = second;
second->next = first_next;
first = first_next;
second = second_next;
}
}